جادوی انتگرال؛ وقتی ریاضی مهار بوستر سوپرهوی اسپیس‌ایکس را ممکن کرد

با فرود دقیق بوستر سوپرهوی، عصر جدیدی در صنعت فضانوردی آغاز شد. در پشت این موفقیت چشمگیر، محاسبات پیچیده‌ی ریاضی نهفته است.

در جهشی تاریخی در صنعت فضانوردی، اسپیس‌ایکس با موفقیت بوسترِ غول‌پیکر سوپرهوی را پس از پرتابِ پنجم استارشیب بازیابی کرد. این دستاوردِ بی‌سابقه که با دقتی شگفت‌انگیز و به‌وسیله‌ی بازوهای مکانیکی مکازیلا محقق شد، پیشرفتِ خیره‌کننده‌ی فناوری موشک‌های قابل‌ استفاده‌ی مجدد را نشان می‌دهد. با این موفقیت، اسپیس ایکس گامی بلند به سوی آینده‌ای برداشته است که در آن، سفرهای فضایی با هزینه‌ی کمتر و فراوانی بیشتر امکان‌پذیر خواهد بود.

اما پشت این موفقیت چشمگیر، محاسبات پیچیده‌ی ریاضی مانند انتگرال، نهفته است؛ بله، همان شاخه‌ای از ریاضی که در دوران دبیرستان برای اکثر ما چیزی جز سردرد و سردرگمی به همراه نداشت! مهندسان اسپیس‌ایکس برای بازگرداندن دقیق و ایمن بوستر سوپرهوی به نقطه‌ی پرتاب، به‌کمک انتگرال، مسیرهای پیچیده‌ی پرواز را محاسبه و تغییرات مداوم نیروها و شرایطِ فرود را پیش‌بینی کردند. انتگرال و محاسبات پیچیده‌ی ریاضی به مهندسان اجازه می‌دهد نیروها، سرعت و موقعیت بوستر را در هر لحظه محاسبه و تنظیم کنند تا بوستر بتواند دقیقاً در مکان تعیین‌شده فرود آید.

بازیابی موفق بوستر سوپرهوی، نه‌تنها یک دستاورد فنی برای اسپیس ایکس محسوب می‌شود، بلکه نمادی از قدرت و اهمیت ریاضیات در فناوری‌های پیشرفته‌ی امروزی است. محاسبات پیچیده‌ای که به کمک انتگرال‌ها انجام می‌شود، نقشی کلیدی در کنترل دقیق مسیرهای پروازی و مهار بوسترها ایفا می‌کند؛ عاملی که می‌تواند سرنوشت پروازهای فضایی را دگرگون و راه را برای مأموریت‌های بزرگ‌تر و جسورانه‌تر باز کند.

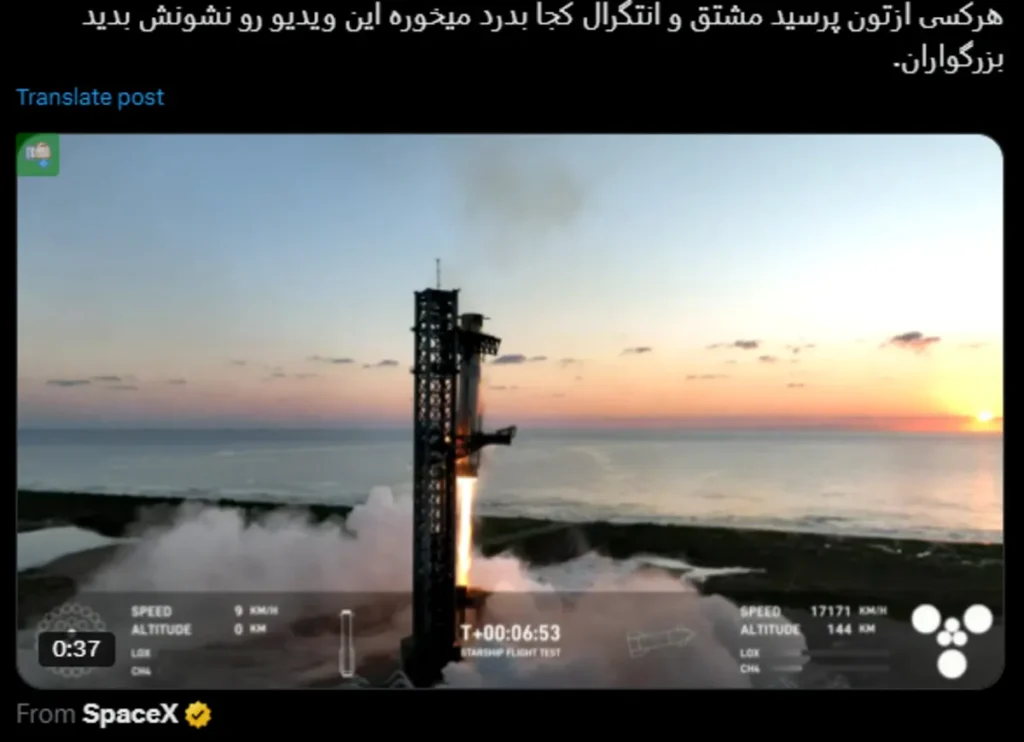
در همین راستا، یکی از کاربران شبکه‌ی ایکس با بازانتشار لحظه‌ی بازیابی بوسترِ غول‌پیکر سوپرهوی پس از پرتابِ پنجم استارشیپ، نوشت: «هرکسی از شما پرسید مشتق و انتگرال کجا به‌درد می‌خورد، این ویدئو را نشانش دهید.» اگر برای شما هم سؤال شده که انتگرال و مشتق به چه دردی می‌خورد و کجای زندگی ما به کار می‌رود، با ما همراه شوید.

به‌طور حتم در دوره‌ی دبیرستان هنگام یادگیری مشتق یا انتگرال از خود پرسیده‌اید، واقعاً چرا باید این مباحث پیچیده و بعضاً گیج‌کننده را یاد بگیرید. آیا واقعاً انتگرال و مشتق یا دیگر مباحث ریاضی کاربردی در زندگی واقعی ما ندارند؟

گالیله، دانشمند و فیزیکدان بزرگ ایتالیایی که به پدر علم مدرن معروف است، معتقد بود که از ریاضیات می‌توان برای رمزگشایی اسرار جهان استفاده کرد. همان‌طور که ما از الفبا برای خواندن و درک کلمات استفاده می‌کنیم، از ریاضیات نیز می‌توانیم برای درک قوانین و الگوهای حاکم بر جهان هستی استفاده کنیم.

بحث خود را با مشتق و کاربرد آن در زندگی واقعی شروع می‌کنیم. مشتق به‌معنای اندازه‌گیری سرعتِ تغییر یک کمیت است. به‌عنوان مثال، هنگام رانندگی برای فهمیدن مقدار سرعت در هر لحظه، باید تغییرات مسافت نسبت به زمان یا مشتق مسافت نسبت به زمان را داشته باشیم. همچنین، شیبِ خط مماس بر نموداری دلخواه در هر نقطه، مشتق تابع در آن نقطه را به ما می‌دهد.

مشتق در علوم و رشته‌های مختلف مانند اقتصاد، فیزیک، نجوم و کامپیوتر استفاده می‌شود. به‌کمک مشتق در اقتصاد می‌توانیم بفهمیم با افزایش تولید یا مصرف، هزینه، درآمد یا سود چگونه تغییر می‌کنند. همچنین، به‌کمک مشتق می‌توانیم نقاط بهینه را پیدا کنیم. به‌عنوان مثال، تولیدکننده‌ای که می‌خواهد بیشترین سود یا کمترین هزینه را داشته باشد، از مشتق برای یافتن سطح بهینه‌ی تولید استفاده می‌کند.

از مشتق‌ و کاربردهای آن در علوم کامپیوتر نمی‌توانیم بگذریم. مشتق نقش مهمی را در پردازش تصویر و خلق تصاویر بهتر ایفا می‌کند. الگوریتم‌های استفاده‌شده در نرم‌افزارهای گوشی‌های هوشمند به کمک مشتق می‌توانند ویژ‌گی‌هایی مانند روشنایی، کنتراست و رنگ‌ها را بهبود بخشند.

مهندسان کامپیوتر همواره به‌دنبال رسیدن به بهترین عملکرد هستند و این کار را با مشتق‌گیری برای بهینه‌سازی الگوریتم‌ها و فرآیندها انجام می‌دهند. به‌عنوان مثال، در بهینه‌سازی موتورهای جست‌وجو یا کاهش مصرف انرژی در مراکز داده، مشتق‌ها کمک می‌کنند تا نقطه‌ای بهینه پیدا شود که در آن الگوریتم یا سیستم با حداکثر کارایی و کمترین هزینه کار کند.

هوش مصنوعی و یادگیری ماشین از مشتق برای یادگیری و بهبود خود استفاده می‌کنند. مشتق به هوش مصنوعی اجازه می‌دهد از تجربیات قبلی خود یاد بگیرد و به‌مرور هوشمندتر شود. شبکه‌های کامپیوتری برای افزایش سرعت و کارایی انتقال داده‌ها، به بهینه‌سازی دائمی نیاز دارند. به‌کمک مشتق می‌توان میزان تغییرات ترافیک شبکه را تجزیه و تحلیل کرد و پیش‌بینی‌هایی انجام داد تا شبکه همیشه در حالت بهینه عمل کند.

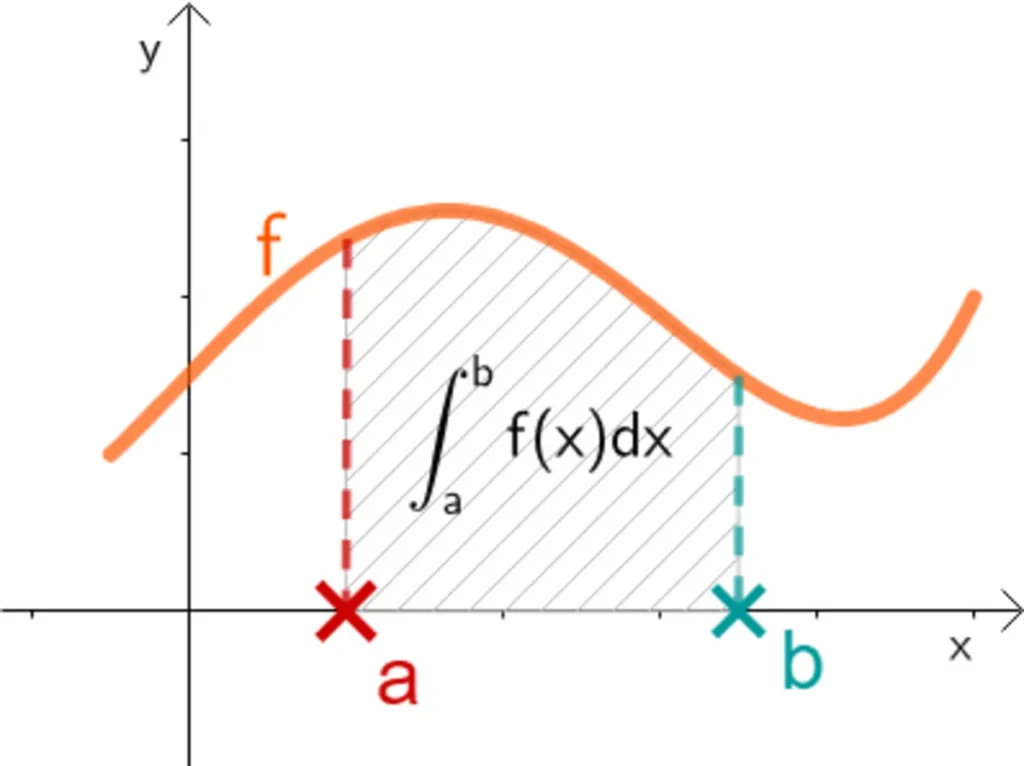
انتگرالِ هر تابع، مساحت زیر نمودار آن تابع را به ما می‌دهد که از این ویژگی‌ می‌توانیم در علوم و فناوری‌های مختلف استفاده کنیم. انتگرال و مشتق عکس یکدیگر هستند. اگر مشتق، تغییرات یک تابع نسبت به کمیتی مانند زمان باشد، انتگرال جمع کل این تغییرات است. مشتق تابعی مانند f(x)=x برابر یک و انتگرالِ یک، برابر x به‌اضافه‌ی مقداری ثابت است. همچنین، اگر از تابعی انتگرال و از پاسخِ انتگرال، مشتق بگیریم، دوباره تابع اولیه را به‌دست می‌آوریم.

به‌کمک انتگرال می‌توانیم حرکت اجسام مختلف را توصیف کنیم. به‌عنوان مثال، با داشتن نمودار تغییرات سرعت جسم برحسب زمان، به‌راحتی می‌توانیم مسافت طی شده توسط جسم را در مدت زمانی مشخص به‌دست آوریم. یافتن احتمال متغیرهای تصادفی و پیوسته یکی دیگر از کاربردهای مهمِ انتگرال است. متغیرهای تصادفیِ پیوسته، مانند دما، هر مقداری را می‌توانند داشته باشند. از این ویژگی می‌توانیم در حل بسیاری از مسائل آمار و احتمال استفاده کنیم.

در فیزیک، انتگرال در زمینه‌های متعددی به کار می‌رود. به‌عنوان مثال، در محاسبه‌ی مرکز جرم و مرکز ثقلِ اجسام پیچیده مانند خودروها و ساختمان‌ها و به‌منظور بهینه‌سازی پایداری و توزیع وزن از انتگرال استفاده می‌کنیم. همچنین، انتگرال کاربرد مهمی در مکانیک سیالات برای محاسبه‌ی جریان، فشار و حجم مایعات دارد.

انتگرال، همچنین نقش بسیار مهمی را در پیشرفت علوم کامپیوتر ایفا می‌کند. انتگرال به ما کمک می‌کند تا تغییرات پیوسته و تدریجی را در سیستم‌های مختلف اندازه‌گیری و تحلیل کنیم. درنتیجه، این توانایی، انتگرال را به ابزاری قدرتمند در حوزه‌های مختلف کامپیوتر تبدیل کرده است.

در گرافیک کامپیوتری، به‌کمک انتگرال می‌توانیم تصاویر سه‌بعدی و جلوه‌های واقع‌گرایانه‌ ایجاد کنیم. به‌عنوان مثال، برای محاسبه‌ی نور و سایه‌ها در صحنه‌ای سه‌بعدی، به محاسبه‌ی انتگرال روی سطوح مختلف نیاز داریم. همچنین، در یادگیری ماشین، انتگرال در بهینه‌سازی مدل‌ها و یادگیری از داده‌ها نقش مهمی دارد. بسیاری از الگوریتم‌های یادگیری ماشین براساس محاسبه‌ی انتگرال‌ها کار می‌کنند. به‌عنوان مثال، در شبکه‌های عصبی، از انتگرال برای محاسبه‌ی خطا و بهینه‌سازی وزن‌های شبکه استفاده می‌شود.

تا اینجا در مورد کاربردهای مشتق و انتگرال به‌صورت جداگانه در حوزه‌های مختلف صحبت کردیم، اما باید بدانیم این دو مبحث از یکدیگر جدا نیستند و ارتباط تنگاتنگی با یکدیگر دارند. این ارتباط تنگاتنگ را می‌توانیم در معادلات دیفرانسیل و حل آن‌ها مشاهده کنیم. به‌کمک این معادلات می‌توانیم بفهمیم طبیعت چگونه کار می‌کند.

معادلات دیفرانسیل مبحثی پیچیده در ریاضیات است و به‌راحتی نمی‌توانیم تمام معادلات به‌دست آمده را حل کنیم، اما حداقل اطلاعات جالبی را از آن‌ها به‌دست می‌آوریم. به‌عنوان مثال، برای به‌دست آوردن مدلی برای رشد جمعیت، حرکت سیالات، توصیف حرکت جسم پس از وارد شدن نیرویی مشخص به آن و رفتار امواج الکترومغناطیسی، از معادلات دیفرانسیل استفاده می‌کنیم.

اکنون اجازه دهید کمی وارد جزئیات شویم و پس از بررسی مثالی از کاربرد معادلات دیفرانسیل در زندگی واقعی، کاربرد این معادلات را هنگامِ پرتاب موشک به فضا و حرکت آن در فضا به‌صورت کلی با یکدیگر بررسی کنیم.

احتمالاً سریال Numb3rs بین سال‌های ۲۰۰۵ تا ۲۰۱۰ را تماشا کرده باشید. در یکی از صحنه‌های سریال، مجری قانون به‌دنبال زوجی است که هنگام سفر به‌دور آمریکا، مرتکب جرم‌های متعددی شده‌اند. پلیس FBI حرکت این زوج را روی نقشه دنبال می‌کند، اما هنوز موفق به دستگیری آن‌ها نشده‌ است. در ادامه‌ی سریال، ریاضی‌دان‌ها با بررسی مسیرِ پیموده شده توسط زوجِ مجرم، به‌کمک منحنی‌ای به‌نام «منحتی تعقیب»‌ (Pursuit Curve) سعی در پیش‌بینی مقصد آن‌ها دارند.

به مسیری که جسم یا موجودی برای تعقیب جسم یا موجودِ دیگر طی می‌کند، منحنی تعقیب می‌گوییم. به بیان ساده‌تر، اگر دو جسم یا موجود داشته باشیم که یکی از آن‌ها (تعقیب‌کننده) دائما به سمت دیگری (هدف) حرکت کند، مسیری که تعقیب‌کننده طی می‌کند تا به هدف برسد، منحنی تعقیب نام دارد.

گربه‌ای را در نظر بگیرید که در تلاش برای گرفتن موشی در حال فرار است. اگر گربه همیشه به سمت مکان فعلی موش حرکت کند، نه به جایی که موش قرار است برود، مسیر حرکت گربه به سمت موش یک منحنی تعقیب خواهد بود. این مسیر معمولاً مستقیم نیست، زیرا موش در حال حرکت است و گربه باید به‌صورت پیوسته مسیر خود را با تغییر موقعیت موش تنظیم کند.

فرص کنید هواپیمایی، هواپیمای دیگری را دنبال می‌کند. برای تعیین مسیرِ هواپیمای تعقیب‌کننده، چند فرض اساسی را در نظر می‌گیریم:

• مسیرِ هدف مشخص است: فرض می‌کنیم هواپیمای تعقیب‌کننده از قبل یک مسیر مشخص دارد که ممکن است مستقیم، مدور یا هر شکل دیگری باشد. این بدان معنا است که مسیرِ حرکتِ هواپیمای هدف کاملاً مشخص است و تغییر نمی‌کند. درنتیجه، هدف طبق مسیری از پیش تعیین شده حرکت می‌کند.
• تعقیب‌کننده همیشه در جهت هدف حرکت می‌کند: فرض دوم آن است که هواپیمای تعقیب‌کننده همیشه به‌سمت مکان فعلی هدف حرکت می‌کند و به مقصدِ هدف در آینده توجهی ندارد.

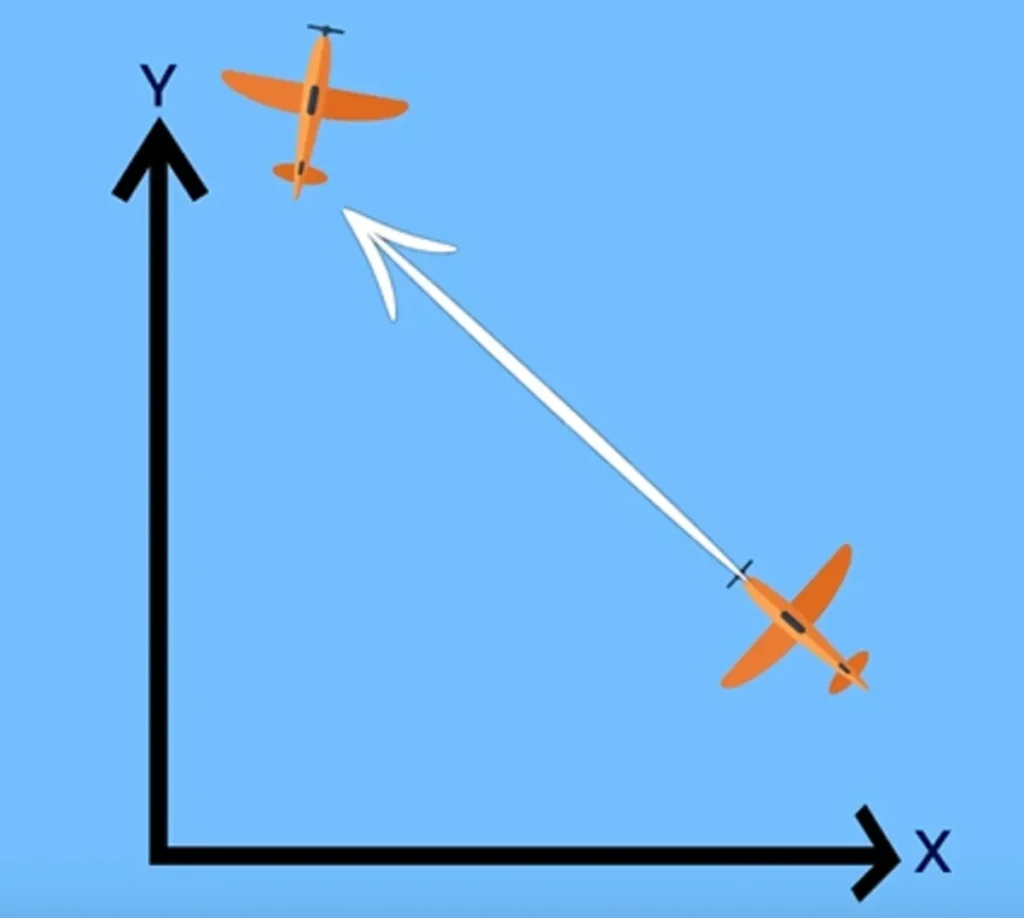
تصویر بالا، لحظه‌ای از پرواز دو هواپیما را نشان می‌دهد. موقعیت هر هواپیما را می‌توانیم به کمک برداری که ابتدای آن مبدأ مختصات و انتهای آن محل فعلی هر هواپیما است، نشان دهیم. همچنین، در هر لحظه از پرواز، نوک یا دماغه‌ی هواپیمای تعقیب‌کننده در جهت هواپیمایی که آن را تعقیب می‌کند، قرار گرفته است. برای درک بهتر و راحت‌تر مثال، هوا را کاملاً صاف و بدون وزش باد در نظر می‌گیریم.

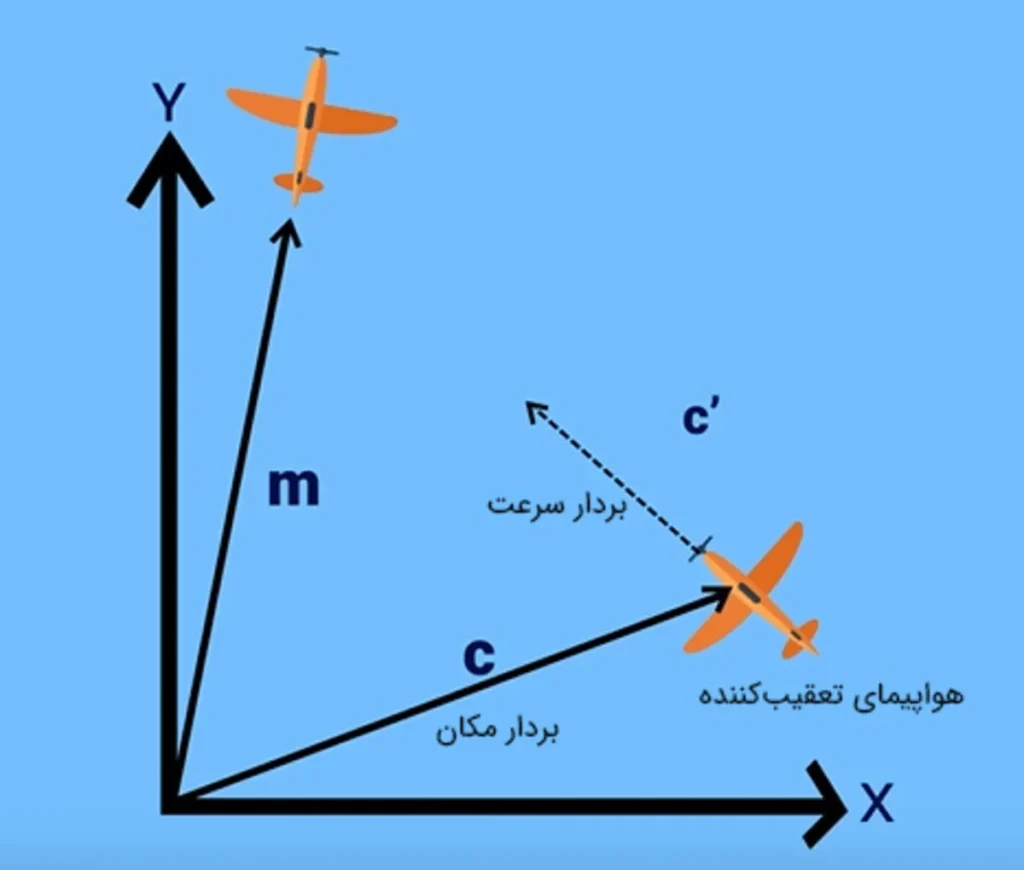
بردار m را در هر لحظه از زمان می‌دانیم، اما مقدارِ بردار c و ‘c (سرعت) را نمی‌دانیم. سرعت از مشتق مکان نسبت به زمان به‌دست می‌آید، بنابراین با دانستن مقدار c در هر لحظه از زمان، به‌راحتی می‌توانیم مقدار بردار c را به‌دست آوریم. با فرض آنکه هواپیمای تعقیب‌کننده با سرعت واحد حرکت می‌کند، می‌توانیم دو معادله‌ی دیفرانسیل بنویسیم و با حل آن‌ها، مقدار c را برحسب زمان به‌دست می‌آوریم.

در سریال Numb3rs، موقعیت دستگیری زوجِ مسافر بسیار پیچیده‌تر از مثالِ دو هواپیما است، اما در پایان به معادلات دیفرانسیلی ختم می‌شود که تقریباً مشابه یکدیگر هستند. اکنون به پرتاب موشک به فضا و کاربرد معادلات دیفرانسیل در این پرتاب برمی‌گردیم.

به‌ احتمال زیاد، پرتاب موشک به فضا را مشاهده کرده‌اید. سوخت موشک از آن خارج و سبب حرکت آن با سرعت بسیار زیادی می‌شود. این حالت مشابه خروج هوا از بادکنک و حرکت بادکنک در جهت مخالفِ خروج هوا است. سوخت با خروج فوق‌العاده سریع از موشک، نیروی بسیار بزرگی به نام نیروی پیشران ایجاد می‌کند که موشک را به سمت جلو می‌راند. سه عامل بر حرکت موشک تأثیر می‌گذارند:

• سرعت خروج گازها: هرچه گازها با سرعت بیشتری از موشک خارج شوند، نیروی پیشران، بزرگ‌تر خواهد بود.
• میزان سوخت مصرفی: هرچه سوخت بیشتری در واحد زمان بسوزد، نیروی پیشران تولیدشده بزرگ‌تر خواهد بود.
• جرم موشک: موشک‌های سبک‌تر با نیروی پیشران یکسان، شتاب بیشتری می‌گیرند.

فرض کنید در زمان صفر و قبل از پرتاب موشک به فضا، جرم آن به‌همراه سوخت برابر m0 است. اگر سوختِ موشک با آهنگ b کیلوگرم‌برثانیه و با سرعت V نسبت به موشک از آن خارج شود، جرم موشک با سوخت باقی‌مانده‌ی داخل آن در زمان t برابر با m0-bt خواهد بود. همچنین، جرم موشک نسبت به زمان با آهنگ b- تغییر می‌کند، زیرا با گذشت زمان و خروج سوخت از موشک، جرم کلی آن کاهش می‌یابد.

طبق قانون دوم نیوتن (حاصل‌ضرب جرم در شتاب برابر نیروی وارد شده بر جسم است)، نیروی پیشران در هر لحظه برابر حاصل‌ضرب جرم موشک در آن لحظه، در شتابِ حرکت آن است. با قرار دادن مقادیر لازم، معادله‌‌ی دیفرانسیل ساده‌ای به‌دست می‌آید که به‌راحتی و با گرفتن انتگرال، سرعتِ موشک را در هر لحظه از زمان به‌صورت زیر به‌دست می‌آوریم:

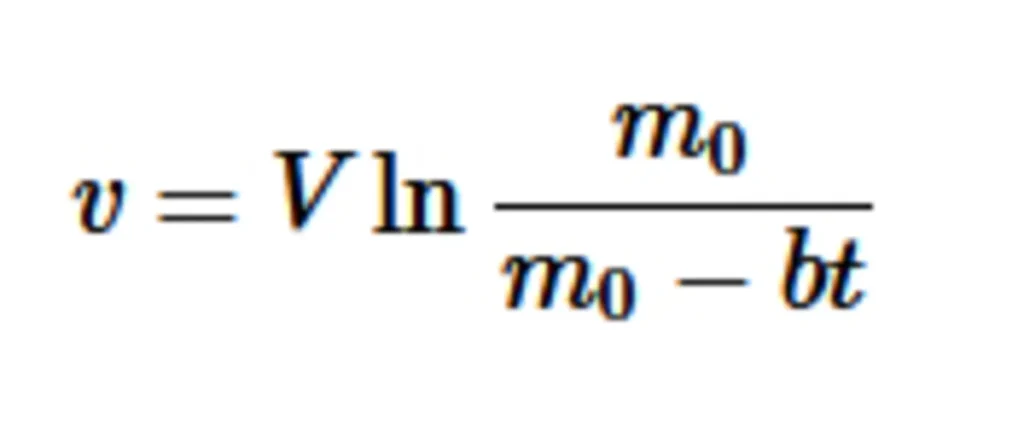
با مشتق گرفتن از رابطه‌ی فوق می‌توانیم شتاب حرکت موشک را نیز در هر لحظه از زمان به‌دست آوریم. همچنین، با گرفتن انتگرال از رابطه‌ی سرعت، مسافت برحسب زمان به‌دست می‌آید. تا اینجا با طرح این مثال بسیار ساده با کاربرد انتگرال و مشتق در حرکت موشک آشنا شدیم. البته نباید فراموش کنیم که در این مثال، از مقاومت هوا و بسیاری از عوامل دیگری چشم‌پوشی کردیم. بنابراین در دنیای واقعی، عوامل متعدی بر پرتاب موشک تاثیر می‌گذارد که باید در نظر گرفته شوند:

• مقاومت هوا: هوا نیرویی در جهت مخالف حرکت هر جسمی، مانند موشک، وارد می‌کند. برای غلبه بر نیروی مقاومت هوا، موشک باید سوخت کافی داشته باشد.
• نیروی جاذبه: موشک برای خارج شدن از جو زمین، باید بر نیروی جاذبه غلبه کند و به سرعتی در حدود ۱۱٫۲ کیلومتربرثانیه برسد. برای محاسبه‌ی سوخت لازم، به‌کمک انتگرال تغییرات مداوم سرعت و نیرو رو را در طول مسیر محاسبه می‌کنیم.
• جرم سوخت و موشک: جرم کل موشک برابر جرم موشک و سوخت است. با افزایش مقدار سوخت، مقدار جرم نیز زیاد می‌شود، بنابراین محاسیات باید بسیار دقیق‌تر انجام شوند.
• مراحل موشک: معمولاً موشک‌ها چند مرحله‌ای طراحی می‌شوند، یعنی بخش‌هایی از موشک بعد از مصرف سوخت و اتمام آن جدا می‌شوند تا جرم کلی کم شود. بنابراین، هنگام محاسبات باید این مورد را نیز در نظر بگیریم.

بازیابی موفق بوستر سوپرهوی اسپیس‌ایکس، شاهکاری از مهندسی و نوآوری است که نشان می‌دهد ریاضیات نقشی کلیدی در پیشرفت فناوری ایفا می‌کند. محاسبات پیچیده‌‌ی نهفته در این دستاورد بزرگ، به ما یادآور می‌شود که ریاضیات، زبانِ ارتباط با جهان و سیله‌ای برای کشف اسرار آن است.

هر یک از ما می‌توانیم با یادگیری ریاضیات، به بخشی از این ماجراجویی بزرگ تبدیل شویم و به حل چالش‌های مهم جهان کمک کنیم. با این دیدگاه شاید یادگیری مباحثی مانند انتگرال، مشتق و معادلات دیفرانسیل را با علاقه‌ی بیشتری دنبال کنیم.

به قلم : سرکار خانم مهدیه یوسفی

منبع : زومیت